GeoSci 236: Orthogonalisation De Gram-Schmidt

Gidon Eshel
491 Hinds
Service des sciences géophysiques,
Avenue 5734 S. Ellis, Univ. de Chicago,
Chicago, Il 60637
(773) 702-0440, mailto:geshel@midway.uchicago.edu


original version


Si nous avons un ensemble de vecteurs linéairement indépendants mais non-orthogonaux ${\bf x}_1$ ${\bf x}_2\cdots{\bf x}_N$ nous souhaitons souvent les transformer en ensemble de vecteurs, $\hat{\bf q}_1$ $\hat{\bf q}_2\cdots\hat{\bf q}_N$ normés, deux à deux orthogonaux,

q}_j de q}_i^T\hat{\bf de \begin{displaymath}\hat{\bf = for}\;\;i\neq j \end{array}\right.\end{displaymath \ de for}\;\;i=j de \left\{\begin{array}{ll}1&{\rm \ 0&{\rm }

La réalisation de cet orthonormalisation est le but du procédé de Gram-Schmidt.

Prenons l'exemple particulier

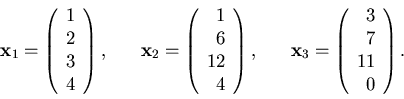
\ du \begin{displaymath}{\bf x}_1=\left(\begin{array}{r}1 \ 2 \ \ 3 \ \ 4\end{array}\righ...... \ de bf x}_3=\left(\begin{array}{r}3 \ 7 \ \ 11 \ \ 0\end{array}\right).\end{displaymath }

Pour le premier vecteur il s'agit d'une normalisation simple;

\begin{displaymath}\hat{\bf q}_1=\frac{1}{\sqrt{{\bf x}_1^T{\bf x}_1}}{\bf x}_1 =...... sqrt{30}}\left(\begin{array}{r}1 \ \ 2 \ \ 3 \ \ 4\end{array}\right).\end{displaymath }

Le deuxième vecteur $\hat{\bf q}_2$ sera le deuxième vecteur initial, ${\bf x}_2$ , moins sa projection sur le premier vecteur $\hat{\bf q}_1$ de la base orthonormale, c'est-à-dire,

\ \sqrt{30}}\left(\begin{array}{r}1 \ 2 \ \ 3 \ \ 4\end{array}\right)\end{displaymath du \begin{displaymath}{\bf q}_2={\bf x}_2-\left({\bf x}_2^T\hat{\bf q}_1\right)\hat...... }


\ du \begin{displaymath}{\bf q}_2=\left(\begin{array}{r}1 \ 6 \ \ 12 \ \ 4\end{array}\rig...... }{6}\left(\begin{array}{r}-7 \ \ 10 \ \ 33 \ \ -28\end{array}\right), \end{displaymath }

ce qui, lors de la normalisation à la norme d'unité, devient

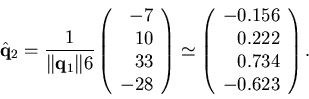
rray}{r \left(\begin{ar du \begin{displaymath}\hat{\bf q}_2=\frac{1}{\Vert{\bf q}_1\Vert 6 }...... } -0,156 \ \ 0,222 \ \ 0,734 \ \ -0,623 \end{array}\right).\end{displaymath }

Pour construire le dernier vecteur de base, nous devons soustraire dede ${\bf x}_3$ ses projections sur $\hat{\bf q}_1$ et $\hat{\bf q}_2$

\begin{displaymath}{\bf q}_3 = { \bf x}_3 -\left({\bf x}_3^T\hat{\bf q}_1\right)\hat{\bf q}_1 -\left({\bf x}_3^T\hat{\bf q}_2\right)\hat{\bf q}_2.\end{displaymath }

Vous épargnant l'arithmétique franchement pénible,

\left(\begin{array}{r du \begin{displaymath}{\bf q}_3\simeq } 2,760 \ \ 1,629 \ \ \end{array}\right)\end{displaymath -0,724 \ \ -0,961 }

cela, une fois normalisé, devient

\begin{displaymath}\hat{\bf q}_3\simeq\left(\begin{array}{r } 0,806 \ \ 0,476 \ \ -0,211 \ \ -0.281\end{array}\right).\end{displaymath }

Pour tester les résultats, nous devons veiller que

orthogonalité de j\;\;\;(\rm de for}\;\;i\neq de \rm du q}_j=\left\{\begin{array}{ll de q}_i^T\hat{\bf de \begin{displaymath}\hat{\bf } 1&{\rm......) \end{array}\right.\end{displaymath }

comme requis.

En conclusion, nous avons transformé notre ensemble initial, non-orthonormal,

\ du \begin{displaymath}{\bf x}_1=\left(\begin{array}{r}1 \ 2 \ \ 3 \ \ 4\end{array}\righ...... \ de bf x}_3=\left(\begin{array}{r}3 \ 7 \ \ 11 \ \ 0\end{array}\right), \end{displaymath }

en un ensemble entièrement équivalent, dont les vecteurs sont orthogonaux 2 à 2 et ont des normes unité.