Retour

Interpolation chaotique

        La transformation réversible d'un vecteur en un vecteur pseudo-aléatoire ou chaotique permet de réaliser une opération d'interpolation approximative mais rapide.
        Le principe de l'interpolation est simple:
        Il suffit d'échantillonner le signal avec un nombre de points différent de l'échantillonnage de départ et de calculer la nouvelle amplitude de chaque point si ce point ne correspond pas à un échantillon du signal d'origine. De nombreuses méthodes sont disponibles qui approximent au mieux l'interpolation théorique.
        Notre approche ne vise pas une efficacité algoritmique mais une démonstration de possibilité de traitement du signal par des méthodes transposables aux circuits neuromimétiques.
        Pour obtenir un nombre d'échantillons inférieur à celui d'origine nous proposons de supprimer des échantillons du signal d'origine et ce de façon aléatoire sur toute la durée du signal. Le nombre de points à supprimer étant proportionnel au rapport signal interpolé sur signal d'origine.
        Nous obtenons ainsi un signal interpolé approximatif en raison du décalage sur l'axe des x des échantillons. Le problème est d'en améliorer la précision .
        Nous répétons donc l'opération avec un échantillonnage aléatoire différent qui décale d'une façon différente les échantillons et nous faisons la moyenne des signaux interpolés obtenus.
        On voit qu'avec des itérations successives les points échantillonnés vont osciller autour d'une valeur moyenne qui sera proche de la valeur désirée.
        Nous présentons ci-dessous le modèle matlab qui réalise cette opération:

Nb_zeros=200; % Le vecteur d'origine comporte 1024 échantillons, le vecteur interpolé 1024-200= 824, rapport=0,80
Iter=200; % Nombre d'itérations
Sum_moy_red=zeros(1,size(Cyc_moy,2)-Nb_zeros); % Initialisation du vecteur somme
        for i=1:Iter
                Cyc_bom=bomb_alea(Cyc_moy,Nb_zeros);
                Cyc_moy_red=[Cyc_moy(find(Cyc_bom)),zeros(1,size(Cyc_bom,2)-Nb_zeros-size(Sum_moy_red,2))]; % suppression des 0
                                                                                                                                                                                 % et ajustement vecteur si nécessaire
                Sum_moy_red=Sum_moy_red+Cyc_moy_red; % Somme des vecteurs réduits
        end
Cyc_moy_red=Sum_moy_red/Iter; % Moyenne
h=figure(1);
set(h,'name','Cycles Origine et Interpolé','resize','off');
axis([1,1024,-1,1]);
hold on;
plot(Cyc_moy);
plot(Cyc_moy_red,'color','r']);

function x=bomb_alea(Cible,Nb_zeros)
% bombardement aléatoire d'un vecteur Cible
% par Nb_zeros

if nargin==0;
       Cible=[1:1:200];Nb_zeros=20; % valeurs d'essai
end

fin=size(Cible,2);
vec_01=ones(1,fin);
position=1;
Nb_points=1;
while Nb_points <= Nb_zeros
         position=floor(rand(1)*(fin-1)+1);
         while vec_01(position)==0
                 position=floor(rand(1)*(fin-1)+1);
         end
         vec_01(position)=0;
         Nb_points=Nb_points+1;
end
x=Cible.*vec_01;


       Dans le programme suivant faisant appel à une transformation chaotique du vecteur, seule la fonction bomb_alea change. On y remarque qu'on "coupe" le vecteur chaotique à la longueur désirée, remplaçant la partie enlevée par des zéros qui seront supprimés par la fonction find( ) de matlab

function x=bomb_alea2(Cible,Nb_zeros)

if nargin==0; % Valeurs d'essai
        Cible=[1:1:200];
        Nb_zeros=20;
end

fin=length(Cible);
pas_premier=primes(2000); % Liste de valeurs premières
n=length(pas_premier);
choix=ceil(rand(1)*n);
pas=pas_premier(choix); % On choisit un pas au hazard dans la liste des nb premiers

while rem(fin+1,pas)==0 % si le pas est un diviseur de fin+1 on tire un nouveau pas
        choix=ceil(rand(1)*n); % ne se produit pas si fin est pair
        pas=pas_premier(choix);
end
for i=1:fin
       position(i)=modulo(i,pas,fin+1); % Vecteur d'adresses
       Cible_crypt(position(i))=Cible(i); % Adressage indexé
end
x_c=[Cible_crypt(1:fin-Nb_zeros),zeros(1,Nb_zeros)]; % Section du vecteur chaotique
x=x_c(position); % Reconstruction du vecteur comprenant Nb_ zeros répartis au hazard


       On remarque que le signal est moins "filtré" avec un échantillonnage chaotique, qui est plus régulier qu'un échantillonnage aléatoire

Nous pouvons appliquer le même principe pour l'agrandissement du signal.

Il s'agit cette fois d'ajouter des échantillons (Nb_zeros) au signal initial (Cible). Chaque échantillon est la moyenne des échantillons adjacents du signal d'origine.

function Vect_augm=bomb_alea3(Cible,Nb_zeros)
% interpolation chaotique agrandissement
if nargin==0; % valeurs par défaut pour tester la fonction
    Cible=[1:1:200];
    Nb_zeros=50;
end
fin=size(Cible,2)+Nb_zeros;
vec_01_org=zeros(1,size(Cible,2)+Nb_zeros);
vec_01_org(1:size(Cible,2))=1;
vec_01=zeros(1,size(Cible,2)+Nb_zeros);
Vect_augm=ones(1,fin);
pas_premier=primes(2000);
n=length(pas_premier);
choix=ceil(rand(1)*n);
pas=pas_premier(choix);
% on choisit un pas au hazard dans la liste des nb premiers
while rem(fin+1,pas)==0 % si le pas est un diviseur de fin+1 on tire un nouveau pas
     choix=ceil(rand(1)*n); % ne se produit pas si fin est pair
     pas=pas_premier(choix);
end
for i=1:fin
     position(i)=modulo(i,pas,fin+1);
     vec_01(position(i))=vec_01_org(i);
end vec_01(1)=1;
vec_01(fin)=1;
curseur=1;
for index=1:fin
     if vec_01(index)~=0
          Vect_augm(index)=Cible(curseur);
          if curseur <= size(Cible,2)-1
               curseur=curseur+1;
          end
     end
     if vec_01(index)==0
           Vect_augm(index)=(Cible(curseur-1)+Cible(curseur))/2; % plateau tant que 0 consécutifs
     end
end
% figure;
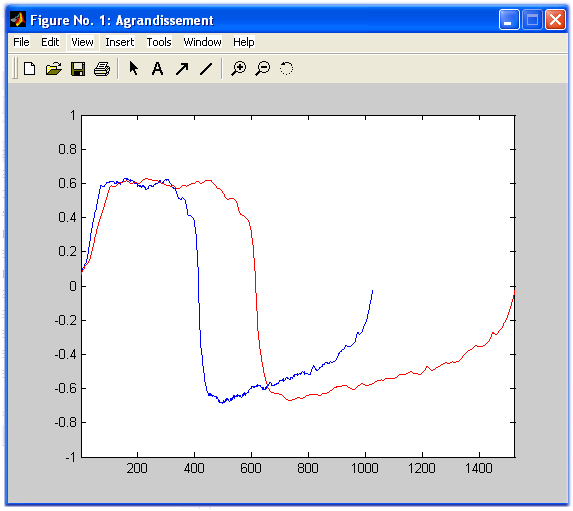
% plot(Vect_augm);

Voici le résultat:

Nb_zeros=500; % Le vecteur d'origine comporte 1024 échantillons, le vecteur interpolé 1024+500=1524, rapport=1.48
Iter=100; % Nombre d'itérations

       Le principe peut bien sûr s'appliquer au traitement d'une image et constituer ainsi un prétraitement complétant l'orthogonalisation nécessaire au stockage maximal sur une mémoire associative. En phase de reconnaissance d'image, la structure en boucle permet de plus le glissement de l'image en modifiant simplement le point de départ de lecture du signal sur la boucle.